Chapter 18 Parameter Estimation

18.1 Normal Distribution

The $\text{normal}$ distribution also known as the Gaussian is perhaps the most well-known distribution. The $\text{normal}$ distribution is typically notated as $N(\mu ,\sigma )$ and has two parameters:

⊕More details for the $\text{normal}$ distribution available on Wikipedia.

1. $\mu$: the mean or central tendency of either your data generating process or your prior uncertainty and,
2. $\sigma$: a measure of spread/uncertainty around $\mu$. Note that for all normally distributed random variables that $\approx$ 95% of realizations fall within a $2\sigma$ band around $\mu$ (i.e. if $X\sim N(\mu ,\sigma )$, then $P(\mu -2\sigma \le x\le \mu +2\sigma )\approx 95\mathrm{\%}$ ) and $\approx$ 99.7% of realizations fall within a $3\sigma$ band (See Figure 18.1).

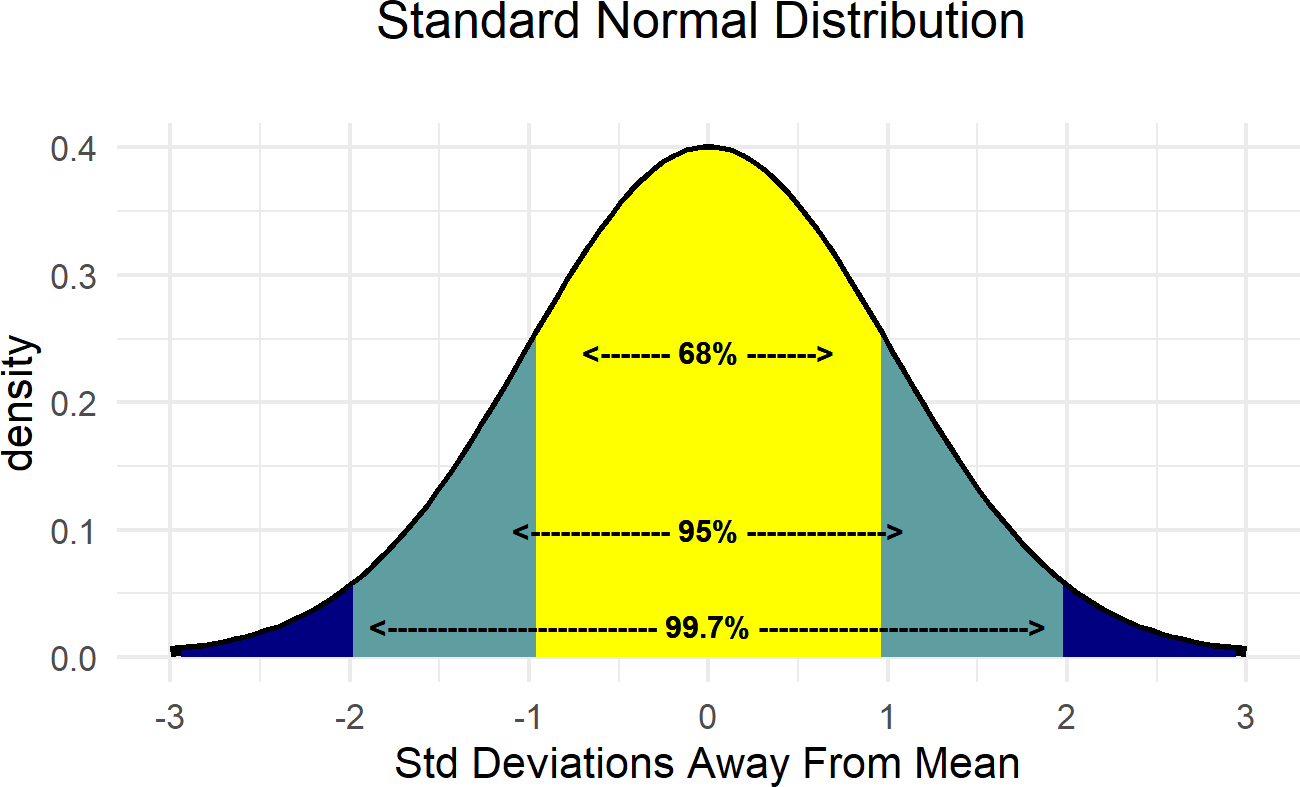Figure 18.1: Demonstrating the relationship between the standard deviation and the mean of the normal distribution.

There is an astounding amount of data in the world that appears to be normally distributed. Here are some examples:

• Finance: Changes in the logarithm of exchange rates, price indices, and stock market indices are assumed normal
• Testing: Standardized test scores (e.g. IQ, SAT Scores)
• Biology: Heights of males in the united states
• Physics: Density of an electron cloud is 1s state.
• Manufacturing: Height of a scooter’s steering support
• Inventory Control: Demand for chicken noodle soup from a distribution center

Due to its prevalance and some nice mathematical properties, this is often the distribution you learn the most about in a statistics course. For us, it is often a good distribution when data or uncertainty is characterized by diminishing probability as potential realizations get further away from the mean. Given the small probability given to outliers, this is not the best distribution to use (at least by itself) if data far from the mean are expected. Even though mathematical theory tells us the support of the $\text{normal}$ distribution is $(-\mathrm{\infty },\mathrm{\infty })$, the probability of deviations far from the mean is practically zero. As such, do not use the $\text{normal}$ distribution by itself to model data with outliers.

Here is just a sample of three normal distributions:

Figure 18.2: Example probability densities of the normal distribution.

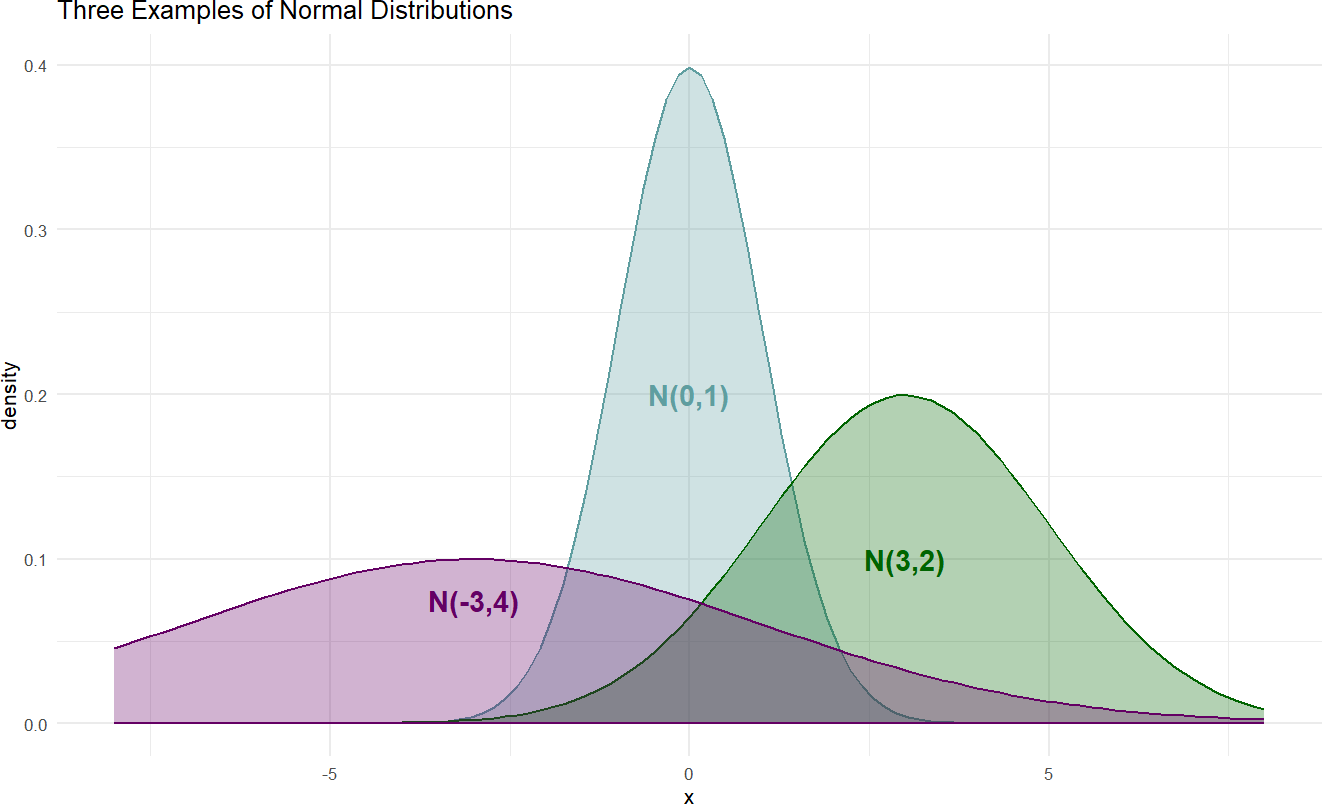
The densities of Figure 18.2 show the typical bell-shaped, symmetric curve, that we are used to. Since the $\text{normal}$ distribution has two parameters, the graphical model representing our uncertainty in the generating process for normally distributed data will have three random variables (see Figure 18.3): 1) the observed data, 2) the mean $\mu$, and 3) the standard deviation $\sigma$.

and the statistical model with priors:

$$\begin{array}{rl}X\sim & N(\mu ,\sigma )\\ \mu \sim & \text{ Some Prior Distribution}\\ \sigma \sim & \text{ Some Prior Distribution}\end{array}$$

where the prior distributions get determined based on the context of the problem under study.

For example, let’s say we are interested in modelling the heights of cherry trees.${}^{\ast \ast }$ ⊕** Looking at the height of cherry trees becasue R has an easily accessible built-in dataset. Even if we do not know much about cherry trees, we can probably be 95% confident that they are somewhere between 1 foot and 99 feet. Hence, we can set up a prior with 95% probability between 1 and 99, i.e. if $X\equiv \text{ Cherry Tree Height}$, then we know that $P(\mu -2\sigma \le x\le \mu +2\sigma )\approx 95\mathrm{\%}$. Hence, we can select $\mu \sim N(50,24.5)$. Note this is a prior on the average height, not the individual height of a cherry tree.

Choosing a prior on $\sigma$ is less intuitive. What do we know about the variation in heights of individual trees? Not much. We can probably bound it though. In fact, we can be 100% certain this is greater than zero; no two cherry trees will be the same height. And I am confident, that cherry tree heights will most definitely fall within say 50 feet of the average, so let’s go with a uniform distribution bounded by 0 and 50.

Hence, our statistical model becomes:

$$\begin{array}{rl}X\sim & N(\mu ,\sigma )\\ \mu \sim & N(50,24.5)\\ \sigma \sim & \text{ Uniform}(0,50)\end{array}$$

After choosing our prior, we then use data to reallocate plausibility over all our model parameters. There is a built-in dataset called trees,

trees %>% as_tibble()

## # A tibble: 31 × 3
##    Girth Height Volume
##    <dbl>  <dbl>  <dbl>
##  1   8.3     70   10.3
##  2   8.6     65   10.3
##  3   8.8     63   10.2
##  4  10.5     72   16.4
##  5  10.7     81   18.8
##  6  10.8     83   19.7
##  7  11       66   15.6
##  8  11       75   18.2
##  9  11.1     80   22.6
## 10  11.2     75   19.9
## # ℹ 21 more rows

which we will use in combination with the following generative DAG:

library(causact)

graph = dag_create() %>%
  dag_node("Tree Height","x",
           rhs = normal(mu,sigma),
           data = trees$Height) %>%
  dag_node("Avg Cherry Tree Height","mu",
           rhs = normal(50,24.5),
           child = "x") %>%
  dag_node("StdDev of Observed Height","sigma",
           rhs = uniform(0,50),
           child = "x") %>%
  dag_plate("Observation","i",
            nodeLabels = "x")

graph %>% dag_render()

Calling dag_numpyro(), we get our representative sample of the posterior distribution:

drawsDF = graph %>% dag_numpyro()

And then, plot the credible values which for our purposes is the 90% percentile interval of the representative sample:

drawsDF %>% dagp_plot()

Figure 18.5: Posterior distribution for the mean and standard deviation of cherry tree heights.

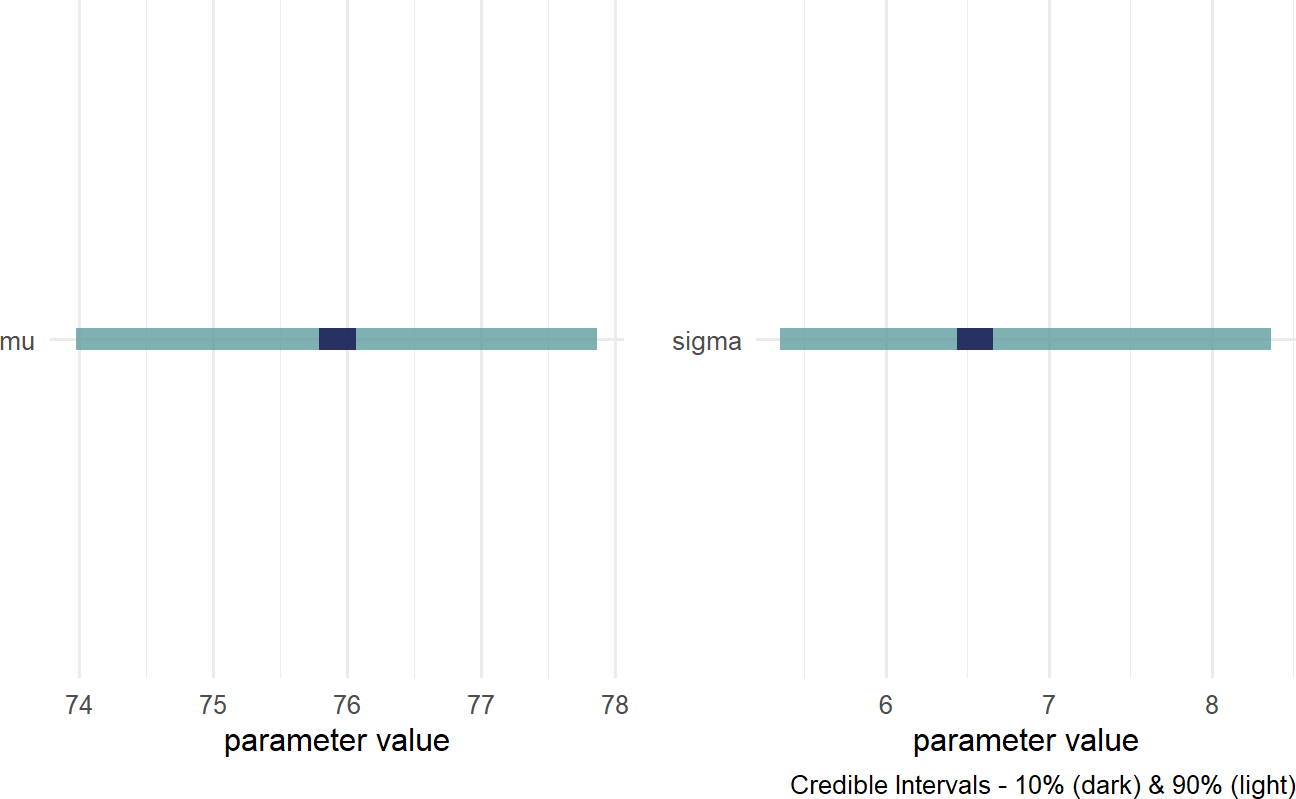
We now have insight as to the height of cherry trees as our prior uncertainty is significantly reduced. ⊕REMINDER: the posterior distribution for the average cherry tree height is no longer normally distributed and the standard deviation is no longer uniform. This is a reminder that prior distribution families do not restrict the shape of the posterior distribution. Instead of cherry tree heights averaging anywhere from 1 to 99 feet as accomodated by our prior, we now say (roughly speaking) the average height is somewhere in the 70-80 foot range. Instead of the variation in height of trees being plausibly as high as 50 feet, the height of any individual tree is most likely within 15 feet of the average height (i.e. $\approx \mu \pm 2\sigma$).

18.2 Gamma Distribution

The support of any random variable with a normal distribution is $(-\mathrm{\infty },\mathrm{\infty })$ which means just about any value is theoretically possible - although values far away from the mean are practically impossible. Sometimes, you want a similar distribution, but one that has constrained support of $(0,\mathrm{\infty })$, i.e. the data is restricted to being strictly positive (even 0 has no density). The $\text{gamma}$ distribution has such support. While the $\text{gamma}$ distribution is often used to fit real-world data like total insurance claims and total rainfall, we will often use this distribution as a prior for another distribution’s parameters. For example, the standard deviation of a normally distributed random variable is strictly positive, so perhaps the Gamma could be appropriate for modelling uncertainty in a standard deviation parameter. Let’s take a deeper look.

⊕More details for the $\text{gamma}$ distribution available at https://en.wikipedia.org/wiki/Gamma_distribution.

The $\text{gamma}$ distribution is a two-parameter distribution notated $\text{gamma}(\alpha ,\beta )$. While there other ways to specify the two parameters, we will use the convention that $\alpha$ refers to a shape parameter and $\beta$ a rate parameter. An intuitive meaning of shape and rate is beyond our needs at this point, for now we just learn those terms because causact expects these two parameters when using a $\text{gamma}$ distribution. Here are some examples of $\text{gamma}$ distributions to get a feel for its shape:

Figure 18.6: Example probability densities of the gamma distribution.

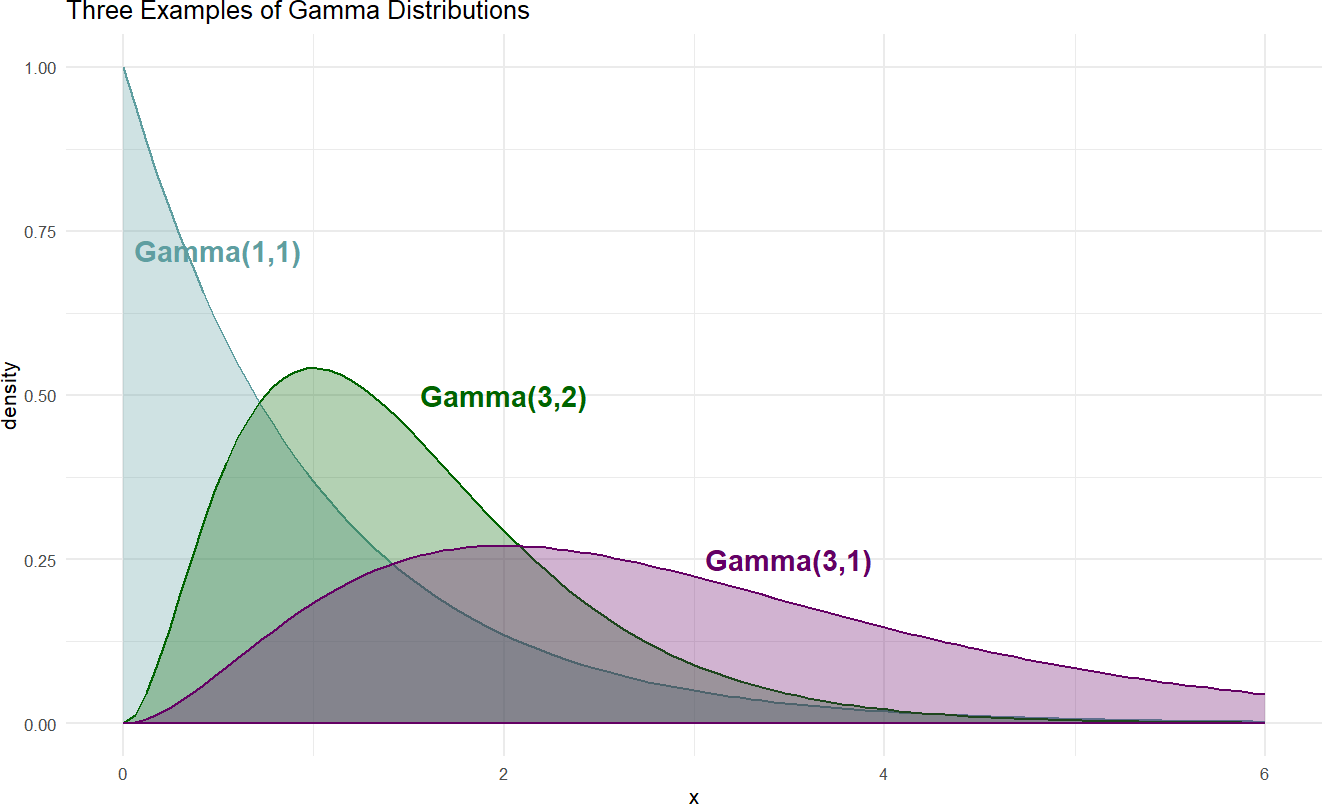
When choosing $\alpha$ and $\beta$ so that our prior uncertainty is accurately represented, we will use a few mathematical properties of the Gamma distribution. Assuming $X\sim \text{gamma}(\alpha ,\beta )$, the following properties are true:

1. $E[X]=\frac{\alpha }{\beta }$: The mean of a Gamma distributed rv is the ratio of $\alpha$ over $\beta$
2. $\text{Var}[X]=\frac{\alpha }{{\beta }^2}$: The variance, a popular measure of spread or dispersion, can also be expressed as a ratio of the two parameters.

⊕The Gamma distribution is a superset of some other famous distributions. The $\text{Exponential}$ distribution can be expressed as $\text{Gamma}(1,\lambda )$ and the $\text{Chi-Squared}$ distribution with $\nu$ degrees of freedom can be expressed as $\text{Gamma}(\frac{\nu }{2},\frac{1}{2})$.

These properties will be demonstrated when the gamma is called upon as a prior in subsequent sections.

18.3 Student t Distribution

For our purposes, the $\text{Student t}$ distribution is a normal distribution with fatter tails - i.e. it places more plausibility to values far from the mean than a similar $\text{normal}$ distribution would. Whereas estimates for the mean of a $\text{normal}$ distribution can get pulled towards outliers, the $\text{Student t}$ distribution is less susceptible to that issue. Hence, for just about all practical questions, the $\text{Student t}$ is a more robust distribution both as likelihood and for expressing prior uncertainty.

The $\text{Student t}$ distribution, as parameterized in causact, is a three parameter distribution; notated $\text{Student-t}(\nu ,\mu ,\sigma )$. The last two parameters, $\mu$ and $\sigma$, can be interpreted just as they are with the normal distribution. The first parameter, $\nu$ (greek letter pronounced “new” and phonetically spelled “nu”), refers to the degrees of freedom. Interestingly, as $\nu \to \mathrm{\infty }$ (i.e. as $\nu$ gets large) the $\text{Student t}$ distribution and the normal distribution become identical; in other words, the fatter tails go away. For all of our purposes, we use a gamma prior for representing our uncertianty in $\nu$ as recommended in https://github.com/stan-dev/stan/wiki/Prior-Choice-Recommendations.

Here is a sample of three student-t distributions:

Figure 18.7: Example probability densities of the Student t distribution.

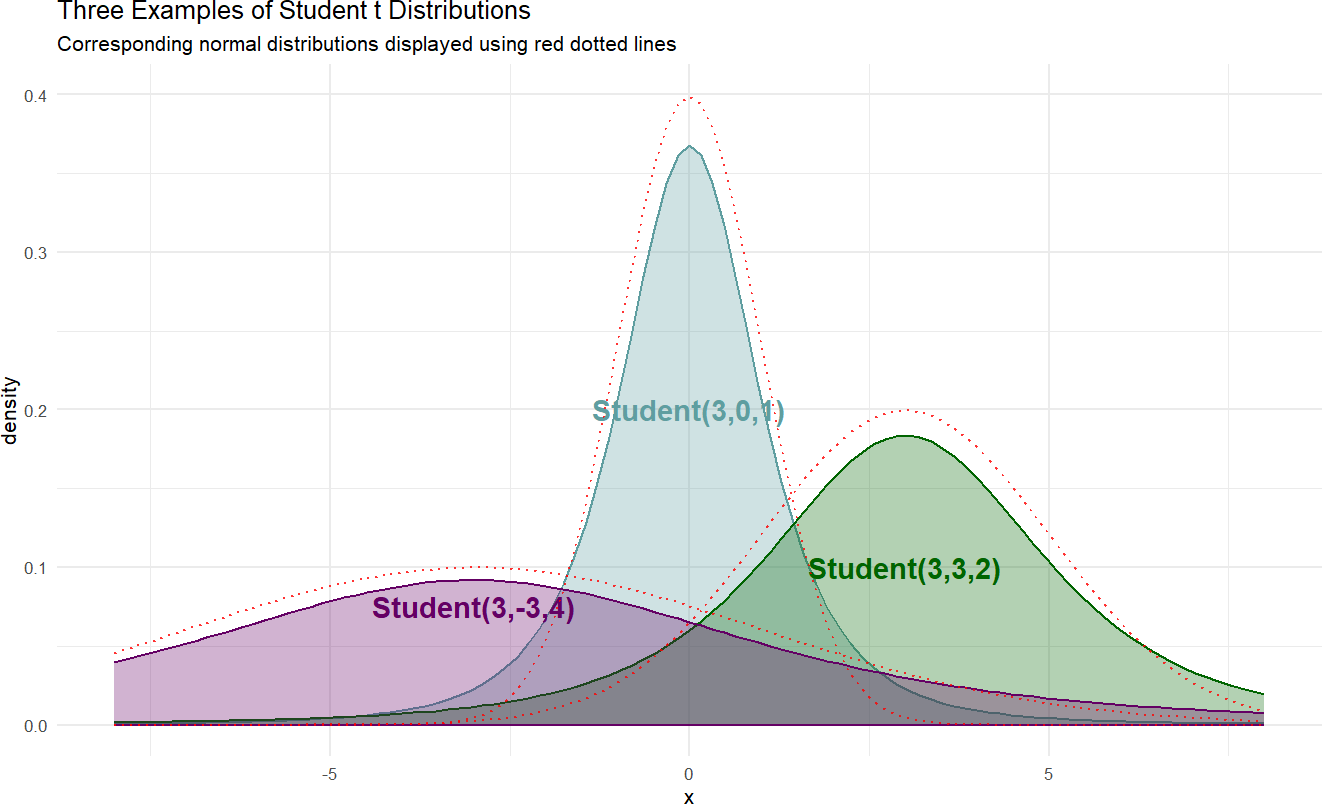
If we wanted to model the cherry tree heights using a $\text{Student t}$ distribution instead of a $\text{normal}$ distribution, the following generative DAG can be used:

library(causact)

graph = dag_create() %>%
  dag_node("Tree Height","x",
           rhs = student(nu,mu,sigma),
           data = trees$Height) %>%
  dag_node("Degrees Of Freedom","nu",
           rhs = gamma(2,0.1),
           child = "x") %>%
  dag_node("Avg Cherry Tree Height","mu",
           rhs = normal(50,24.5),
           child = "x") %>%
  dag_node("StdDev of Observed Height","sigma",
           rhs = uniform(0,50),
           child = "x") %>%
  dag_plate("Observation","i",
            nodeLabels = "x")

graph %>% dag_render()

Calling dag_numpyro(), we get our representative sample of the posterior distribution:

drawsDF = graph %>% dag_numpyro()

And then, plot the credible values to observe very similar results to those using the $\text{normal}$ distribution:

drawsDF %>% dagp_plot()

Figure 18.9: Posterior distribution for the mean, standard deviation, and degrees of freedom when modelling cherry tree heights.

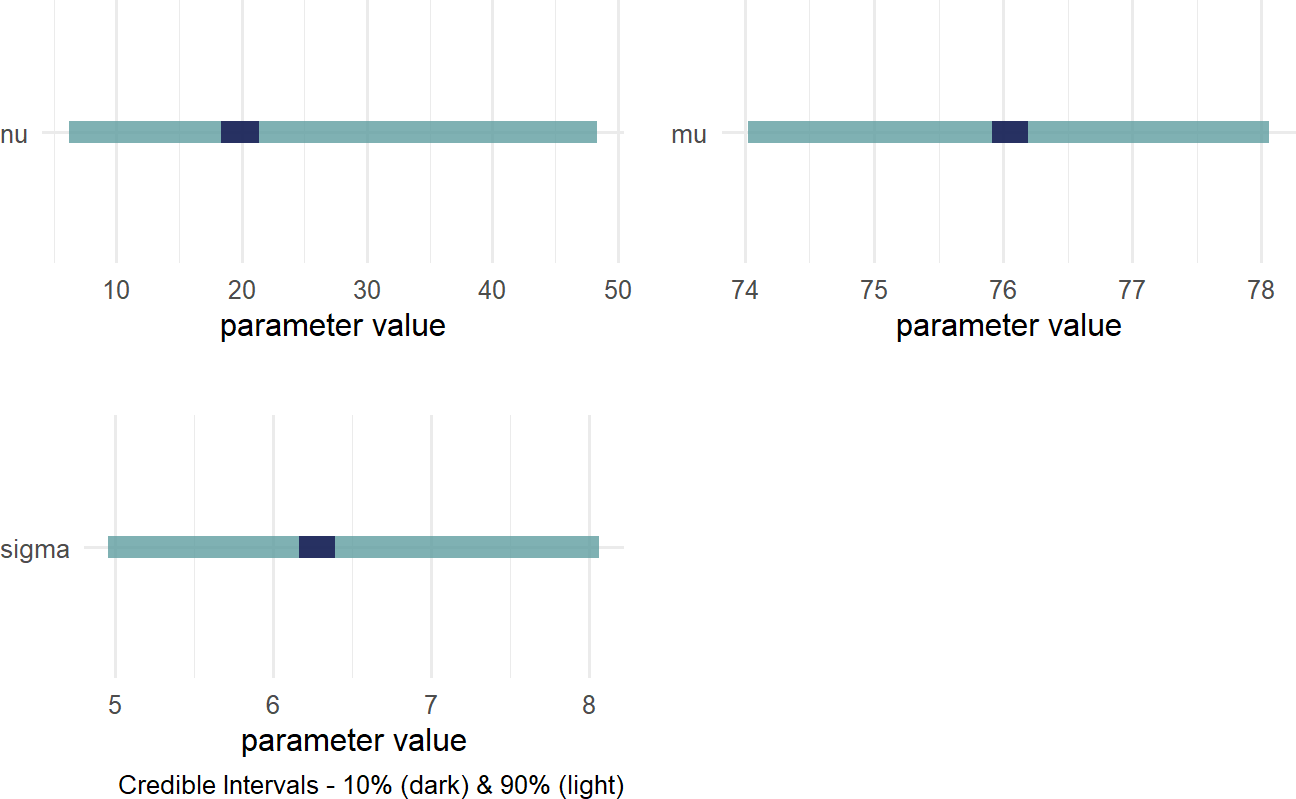
The wide distribution for $\nu$ can be interpreted as saying we do not know how fat the tails for this distribution should be. Which makes sense! You need alot of data to potentially observe outliers, so with only 31 observations our generative model remains uncertain about this degrees of freedom parameter.

18.3.1 Robustness Of Student t Distribution

To highlight the robustness of the $\text{Student-t}$ distribution to outliers and the lack of robustness of the $\text{normal}$ distribution, let’s add a mismeasured cherry tree height to the data. While most heights are between 60-80 feet, a mismeasured and truly unbelievable height of 1,000 is added to the data (i.e. dataWithOutlier = c(trees$Height,1000)). Figure 18.10 shows recalculated posterior densities for both the normal and student t priors.

Figure 18.10: Estimates of a distributions central tendency can be made to downplay outliers by using a student t prior distribution for the mean.

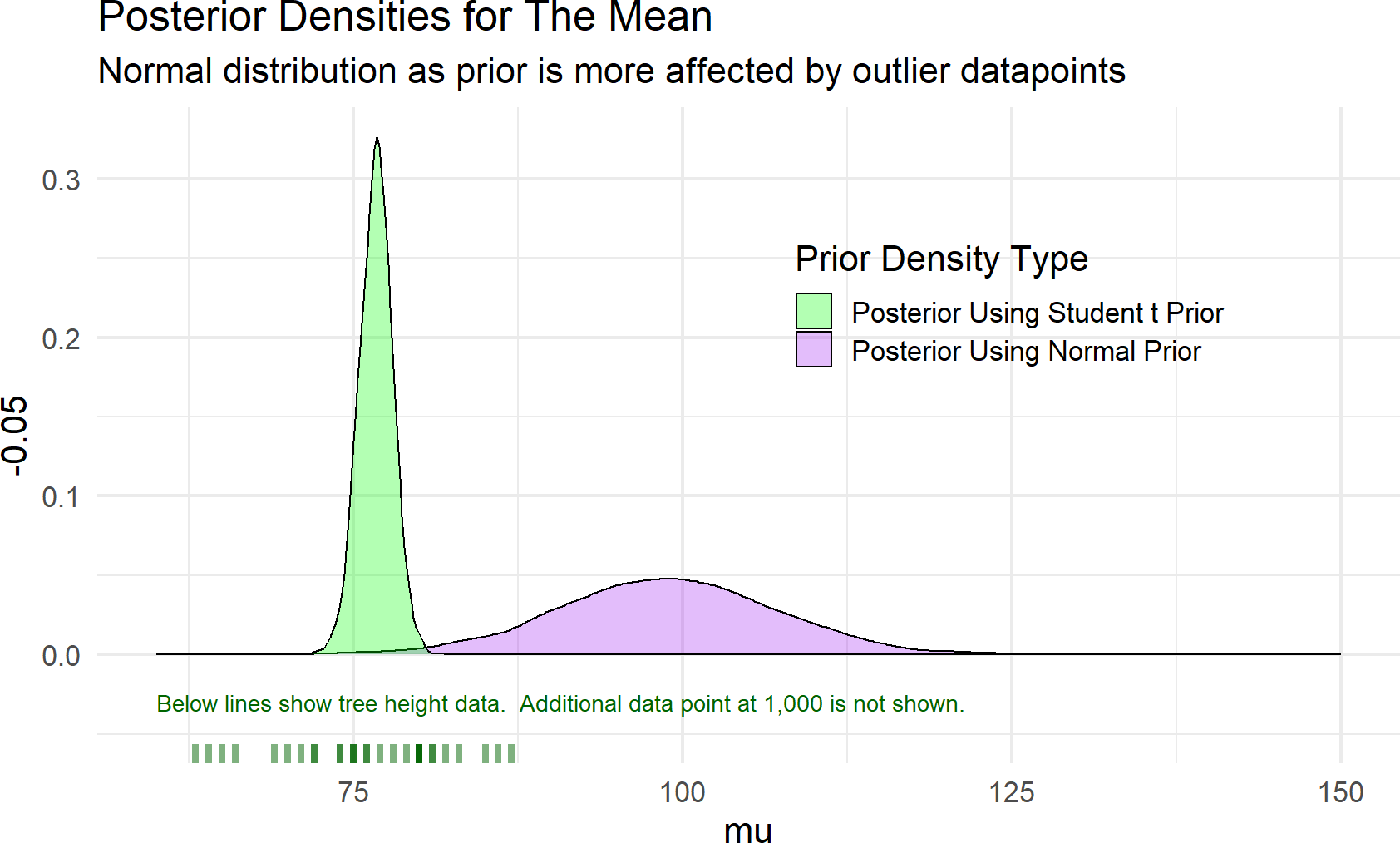
As seen in Figure 18.10, the posterior estimate of the mean when using a $\text{normal}$ prior is greatly affected by the outlier data point - the posterior average height gets concentrated around an absurd 100 feet. Whereas, the $\text{Student-t}$ prior seems to correctly ignore that mismeasured data and concentrates the posterior expectation of average cherry tree height around 76 (as discovered previously). While in this case, ignoring the outliers is desirable and the student t distribution provides a robust method for discounting outliers, all modelling choices should be made so that the posterior distribution accurately reflects your prior expectations of how data should be mixed with prior knowledge.

18.4 Poisson Distribution

The Poisson distribution is useful for modelling the number of times an event occurs within a specified time interval. It is a one parameter distribution where if $K\sim \text{Poisson}(\lambda )$, then any realization $k$ represents the number of times an event occurred in an interval. The parameter, $\lambda$, has a nice property in that it is a rate parameter representing the average number of times an event occurs in a given interval. Given this interpretability, estimating this parameter is often of interest. A graphical model for estimating a Poisson rate from count data is shown below:

and a prior for $\lambda$ will be determined by the use case. For an example, let’s use the ticketsDF dataset in the causact package.${}^{\ast \ast }$

⊕There are several assumptions about Poisson random variables that dictate the appropriateness of modelling counts using a Poisson random variable. Three of those assumptions are: 1) $k$ is a non-negative integer of counts in a specified time interval, 2) the rate $\lambda$ at which events occur is constant, and 3) the occurrence of one event does not affect the probability of additional events occurring (i.e. events are independent). As an example of violating the second assumption, it would not be appropriate to model arrivals per hour to a restaurant as a Poisson random variable because the rate of arrivals certainly varies with time of day (e.g. lunch, dinner, etc.)

Let’s create a dataframe of tickets issued on Wednesday’s in New York City, and then model the rate of ticketing on Wednesdays using the Poisson likelihood with appropriate prior.

library(causact)
library(lubridate)
nycTicketsDF = ticketsDF

## summarize tickets for Wednesday
wedTicketsDF = nycTicketsDF %>% 
  mutate(dayOfWeek = wday(date, label = TRUE)) %>%
  filter(dayOfWeek == "Wed") %>% ## note "=="
  group_by(date) %>% ## aggregate by date
  summarize(numTickets = sum(daily_tickets))

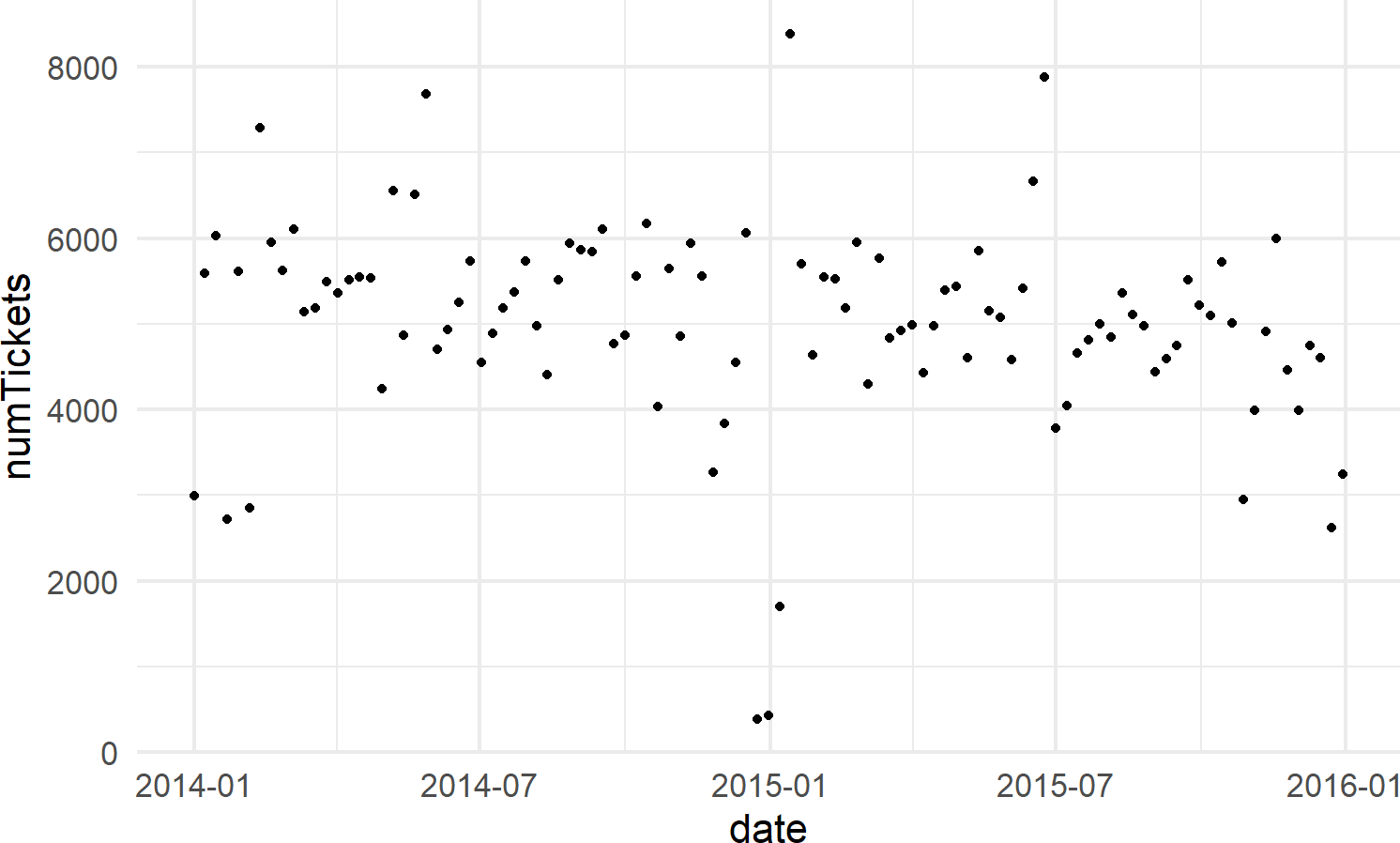
# visualize data
ggplot(wedTicketsDF, aes(x = date, y = numTickets)) + 
  geom_point()

Figure 18.12: The number of daily traffic tickets issued in New York city from 2014-15.

Now, we model these two years of observations using a Poisson likelihood and a prior that reflects beliefs that the average number of tickets issued on any Wednesday in NYC is somewhere between 3,000 and 7,000; for simplicity, let’s choose a $\text{Uniform}(3000,7000)$ prior as in the following generative DAG:

graph = dag_create() %>%
  dag_node("Daily # of Tickets","k",
           rhs = poisson(rate),
           data = wedTicketsDF$numTickets) %>%
  dag_node("Avg # Daily Tickets","rate",
           rhs = uniform(3000,7000),
           child = "k")

graph %>% dag_render()

And extracting our posterior for the average rate of ticket issuance, $\lambda$ (NOTE: we use rate in code instead of lambda due to the latter being a reserved word in Python that will cause issues with using dag_numpyro()), yields the following posterior:

drawsDF = graph %>% dag_numpyro()
drawsDF %>% dagp_plot()

Figure 18.14: Posterior density for uncertainty in the rate parameter.

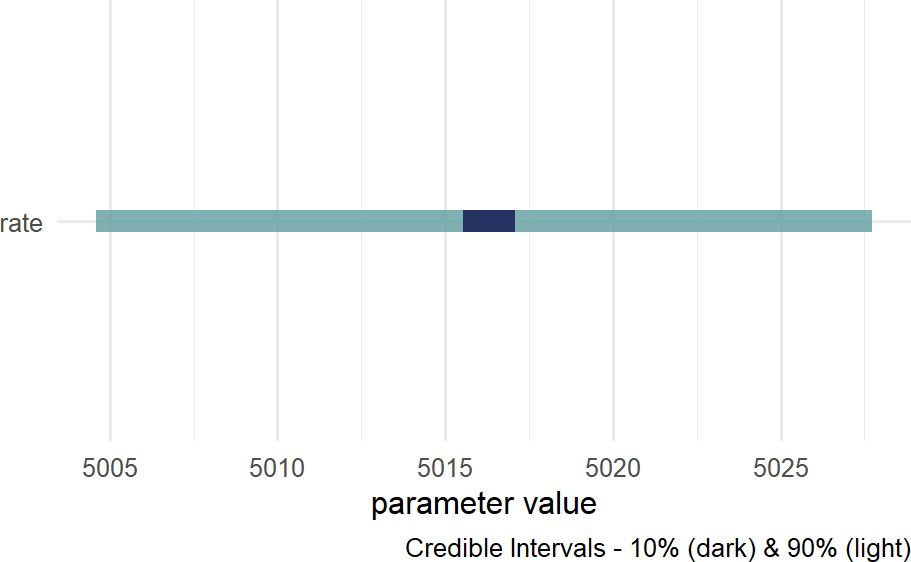
where we see that that the average rate of ticketing in NYC is somewhere slightly more than 5,000 tickets per day.

18.5 Exercises

library(tidyverse)
tDF = readr::read_csv(
  file = "https://raw.githubusercontent.com/flyaflya/persuasive/main/estimateTheT.csv",
  show_col_types = FALSE)

Figure 18.15: Generative dag for a student t-distribution.

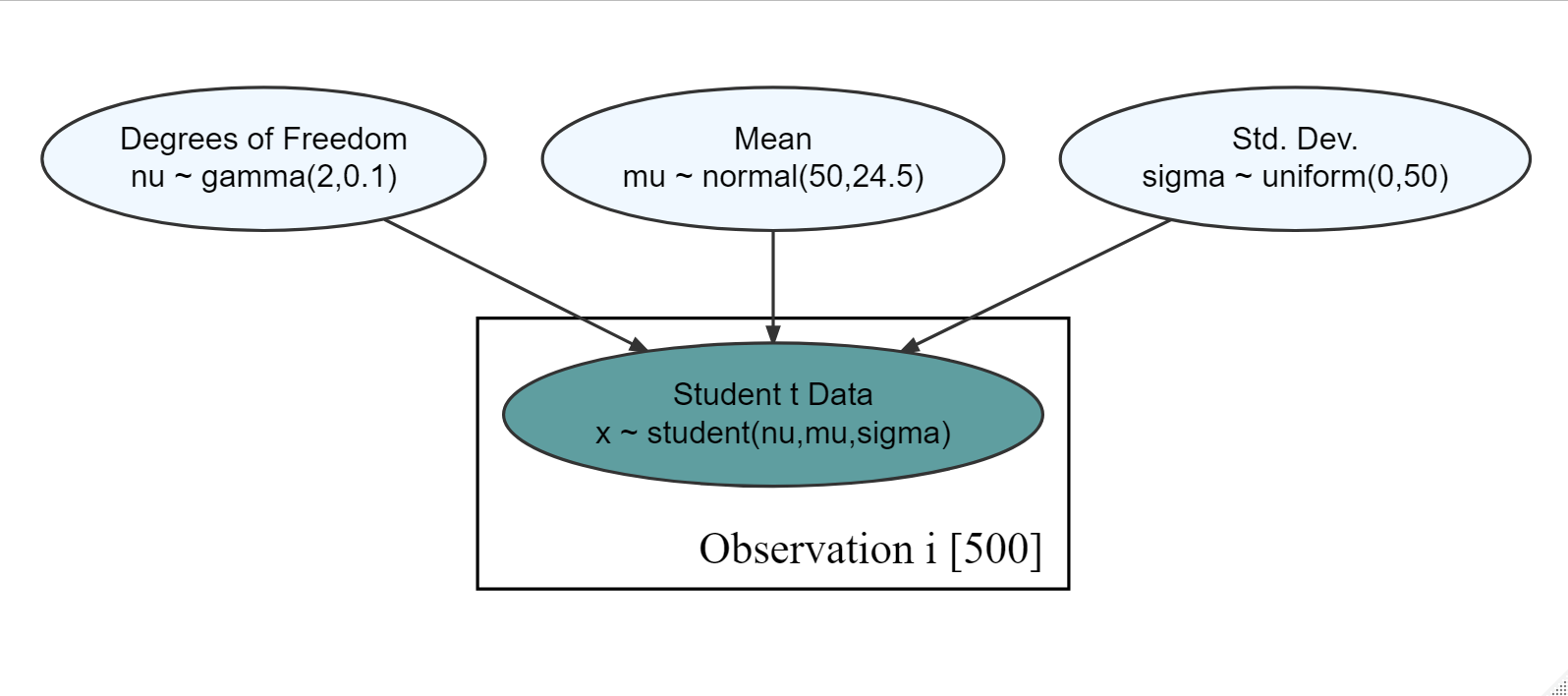
Based on the observational model in Figure 18.15 and the observed data in tDF, what is your posterior estimate that the mean ($\mu$) is greater than 46? Report your probability estimate as a decimal rounded to the nearest tenth. (e.g. 0.10, 0.50, 0.90, etc.)

library(tidyverse)
tDF = readr::read_csv(
  file = "https://raw.githubusercontent.com/flyaflya/persuasive/main/titanic.csv",
  show_col_types = FALSE)

Figure 18.16: Generative dag for a student t-distribution.

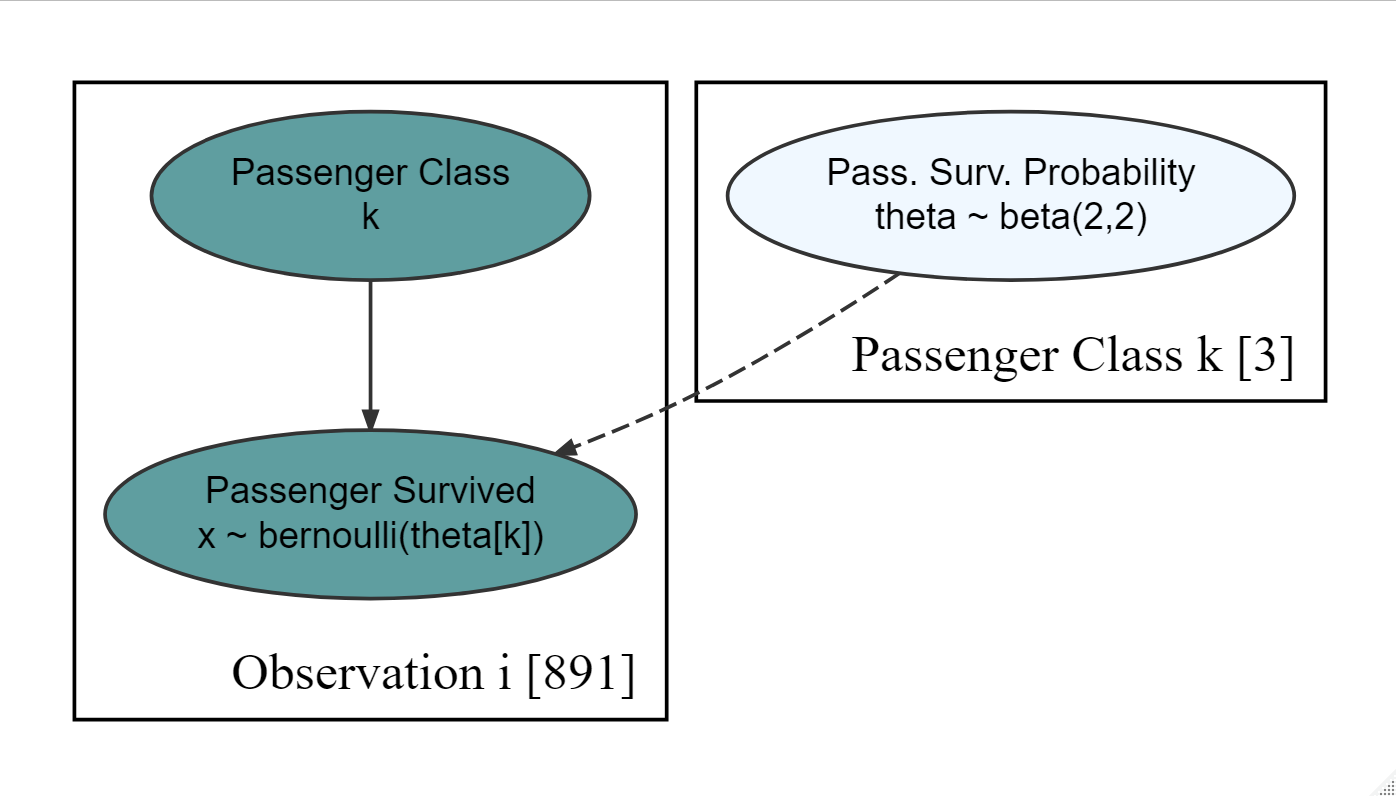
Using the generative DAG of Figure 18.16, estimate the probability that ${\theta }_1\ge ({\theta }_2+0.10)$. In other words, did people in first class on the Titanic have at least a 10% increase in survival chances over those passengers in 2nd class? Report your probability as a decimal rounded to the nearest hundredths place (e.g. 0.12, 0.44,0.50,0.99, etc.)

Figure 18.17: Histogram of runs scored per game at the Colorado Rockies stadium.

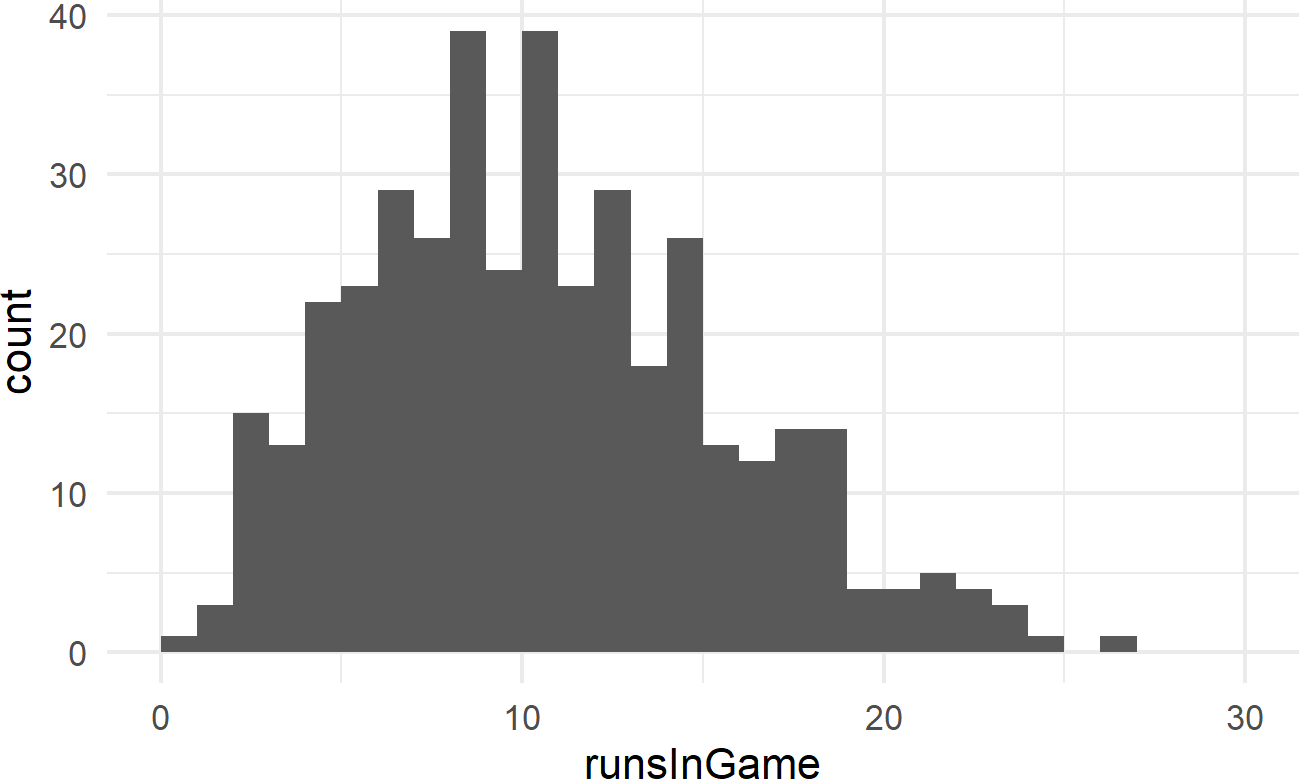
Runs scored per game is a good example of count data. And often, people will use a Poisson distribution to model this type of outcome in sports.

graph = dag_create() %>% 
  dag_node("Avg. Runs Scored","rate",
           rhs = uniform(0,50)) %>% 
  dag_node("Runs Scored","k",
           rhs = poisson(rate),
           data = baseDF$runsInGame) %>% 
  dag_edge("rate","k") %>% 
  dag_plate("Observation","i",
            nodeLabels = "k")
graph %>% dag_render()

Using the generative DAG of Figure 18.18, what is the probability that the “true” average number of runs scored at Colorado’s Coors Field ballpark is at least 11 runs per game? (i.e. $rate>11$). Report your probability as a decimal rounded to the thousandths place (e.g. 0.120, 0.510, 0.992, etc.)